In previous blog Complexity of Python Operations, I noticed that the way that Richard used to solve the biggest K problem by heap is arguable.

Richard’s statement

He mentioned that, in order to

use priority to find the 10 biggest (of N) values: we would enqueue N values and then dequeue 10 values.

There are two methods to compare with,

• Implementation 1: Add each new value into an array (complexity = O(1)) for N times, and remove the highest priority value (complexity = O(N)) for 10 times. $$O(1) * N + O(N) * 10 = O(N)$$
• Implementation 2: Add each new value into a heap (complexity = O(logN)) for N times, and remove the highest priority value (complexity = O(logN)) for 10 times. $$O(logN) * N + O(logN) * 10 = O(N logN)$$

Therefore, the conclusion is,

So, as N gets bigger, Implementation 1 will eventually become faster … for the “find the 10 biggest” task.

Questions

The most questionable part is: Is the cost of building a heap as high as O(NlogN) ?

As we all know the time complexity of heapsort is also O(NlogN), however, by heapsorting an array, all the elements are sorted. Then why should we perform an operation, that is close to heapsort, to find top $K$ elements?

It’s not necessary. The answer is No.

There are two ways two initialize a heap:

1. Heapify the whole tree, everytime when one new value added.
2. Heapify the whole tree, after all values are added.

Obviously the first option will cause no less operations than the second one. Such operation differences can be visualized in Visualgo.net.
Notice there are two options in left bottom menu:

• Create(A) - O(N log N)
• Create(A) - O(N)

The results after heapifying [2,7,26,25,19,17,1,90,3,36] are plotted as following trees,

Different forms of heaps, and both legal. These example is another strong evidence for:

Heap is a partly-sorted structure.

These options reflect two corresponding ways, and it’s contrary to intuition that the second option has time complexity as low as $O(N)$.

Why is the cost of building a heap O(N) ?

Explaination

I will quote explaination from Emre nevayeshirazi,

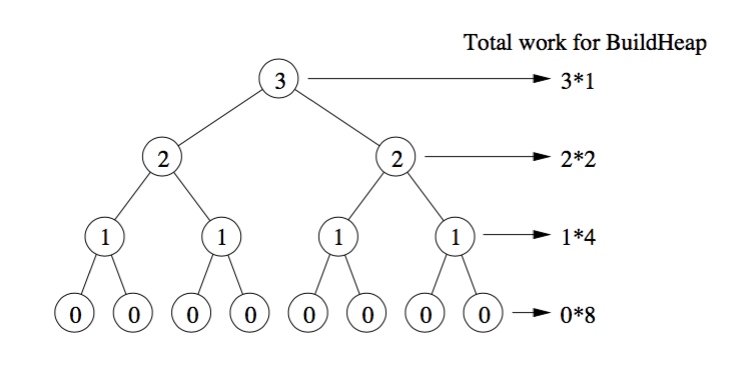
The main idea is that in the build_heap algorithm the actual heapify cost is not O(log N) for all elements.

When heapify is called, the running time depends on how far an element might move down in tree before the process terminates. In other words, it depends on the height of the element in the heap. In the worst case, the element might go down all the way to the leaf level.

Let us count the work done level by level.

At the bottommost level, there are $2^{h}$ nodes, but we do not call heapify on any of these, so the work is 0. At the 2nd level from the bottom are $2^{h − 1}$ nodes, and each might move down by 1 level. At the 3rd level from the bottom, there are $2^{h − 2}$ nodes, and each might move down by 2 levels.

As you can see not all heapify operations are O(log N).

Given a tree with $N$ nodes, the maximum height of a balanced tree, such as a heap tree, $H = Math.ceil(log N)$. In other words,

$$ N \le 2^{H+1} $$

Then, we sum up times of swapping operation, from 1 level above bottom, to the top most level. In $h$-th level, there are $2^{H-h}$ nodes to be handled. Thus, total complexity is

$$\sum_{h=1}^H h * 2^{H-h} = 2^H * \sum_{h=1}^H \frac{h}{2^{h}} \approx \frac{N}{2} * S$$
where we define,
$$ S = \sum_{h=1}^H \frac{h}{2^{h}} = \frac{1}{2} + \frac{2}{4} + \frac{3}{8} + … \frac{H}{2^H}$$

And $S$ has a limit, plotted as follows,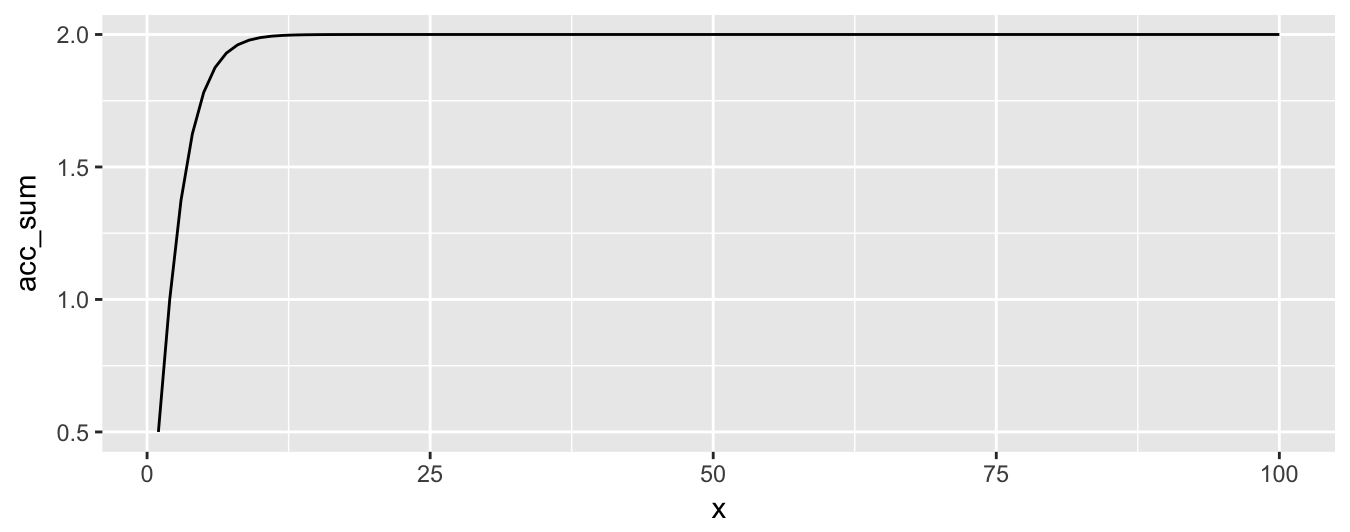

$$ \lim_{x\to\infty} S = 2 $$

We can come to a conclusion that,

The time complexity of building a heap is O(N).

Back to finding K biggest

First, add each element into an array, which will cost O(N).

Second, build a max heap from nodes in 1-level above bottom. Traverse over these nodes, with index less than half of the total amount, will cost O(N).

Third, extract the top node, and re-heapify after each extraction, which will cost O(logN * K).

In total, it costs $O(2 N + K logN)$ operations.

As N/K grows, heap enhanced implementation keeps a stable and low time complexity.

Keep a heap of size K

Another idea will be only to keep biggest K elements known so far, as a min heap. Every time when the new value is bigger than the smallest one in heap, we replace and re-heapify. This solution only requires one traversal of the array.

The overall complexity is $O(logK) * O(N) = O(N log K)$. This solution requires much smaller space but in exchange it will take longer time.

But still, heap enchanced solution outperforms the $O(NK)$ solution.

Heap rocks! Richard’s conclusion is not true, as an example for sometimes there is not a “best all the time” implementation, his statement is not accurate.