
Complexity of Python Operations
This article Complexity of Python Operations has a clear and inspiring explanation of computation complexity.
I really like the way it analyses problems, especially the section for Priority Queue. I reformat the whole article to Markdown as follows.
Complexity of Python Operations
Author: Richard E. Pattis
https://www.ics.uci.edu/~pattis/ICS-33/lectures/complexitypython.txt
In this lecture we will learn the complexity classes of various operations on Python data types. Then we will learn how to combine these complexity classes to compute the complexity class of all the code in a function, and therefore the complexity class of the function. This is called “static” analysis, because we do not need to run any code to perform it (contrasted with Dynamic or Empirical Analysis, when we do run code and take measurements).
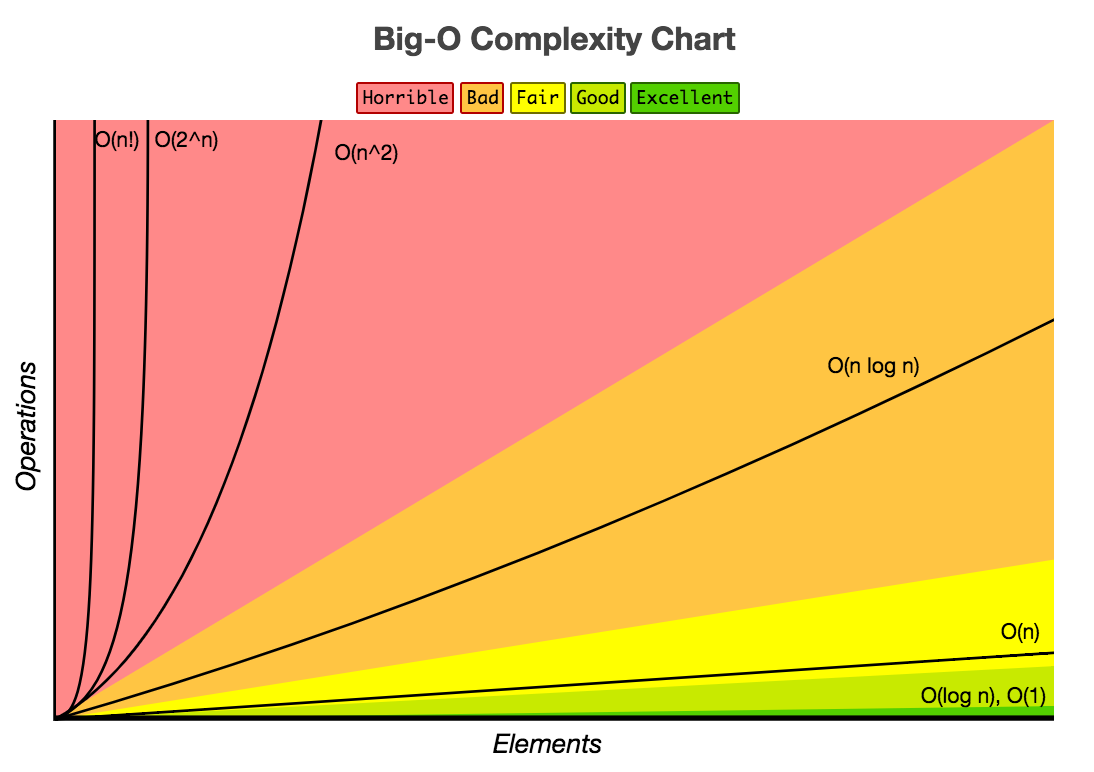
Python Complexity Classes
In ICS-46 we will write low-level implementations of all of Python’s data types and see/understand WHY these complexity classes apply. For now we just need to try to absorb (not memorize) this information, with some -but minimal- justification.
Binding a value to any name (copying a reference) is O(1). Simple operators on integers (whose values are small: e.g., under 12 digits) like + or == are also O(1).
In all these examples, N = len(data-type). The operations are organized by increasing complexity.
Lists:
| Operation | Example | Complexity Class | Notes |
|---|---|---|---|
| Index | l[i] | O(1) | |
| Store | l[i] = 0 | O(1) | |
| Length | len(l) | O(1) | |
| Append | l.append(5) | O(1) | |
| Pop | l.pop() | O(1) | same as l.pop(-1), popping at end |
| Clear | l.clear() | O(1) | similar to l = [] |
| Slice | l[a:b] | O(b-a) | l[1:5] : O(1) l[:] : O(len(l)-0)=O(N) |
| Extend | l.extend(…) | O(len(…)) | depends only on len of extension |
| Construction | list(…) | O(len(…)) | depends on length of … |
| check ==, != | l1 == l2 | O(N) | |
| Insert | l[a:b] = … | O(N) | |
| Delete | del l[i] | O(N) | |
| Remove | l.remove(…) | O(N) | |
| Containment | x in/not in l | O(N) | searches list |
| Copy | l.copy() | O(N) | Same as l[:] which is O(N) |
| Pop | l.pop(i) | O(N) | O(N-i) l.pop(0):O(N) (see above l.pop(-1):O(1) ) |
| Extreme value | min(l)/max(l) | O(N) | searches list |
| Reverse | l.reverse() | O(N) | |
| Iteration | for v in l: | O(N) | |
| Sort | l.sort() | O(N Log N) | key/reverse mostly doesn’t change |
| Multiply | k*l | O(k N) | 5*l : O(N) len(l)*l : O(N^2) (Kai’s comment: correct but confusing) |
Tuples support all operations that do not mutate the data structure (and with the same complexity classes).
Sets:
| Operation | Example | Complexity Class | Notes | |
|---|---|---|---|---|
| Length | len(s) | O(1) | ||
| Add | s.add(5) | O(1) | ||
| Containment | x in/not in s | O(1) | compare to list/tuple - O(N) | |
| Remove | s.remove(5) | O(1) | compare to list/tuple - O(N) | |
| Discard | s.discard(5) | O(1) | ||
| Pop | s.pop(i) | O(1) | compare to list - O(N) | |
| Clear | s.clear() | O(1) | similar to s = set() | |
| Construction | set(…) | O(len(…)) | depends on length of … | |
== , != |
s != t | O(len(s)) | same as len(t): False in O(1) if the lengths are different | |
<= , < |
s <= t | O(len(s)) | issubset (s <= t) == (t >= s) | |
>= , > |
s >= t | O(len(t)) | issuperset | |
| Union | s | t | O(len(s)+len(t)) | |
| Intersection | s & t | O(len(s)+len(t)) | ||
| Difference | s - t | O(len(s)+len(t)) | ||
| Symmetric Diff | s ^ t | O(len(s)+len(t)) | ||
| Iteration | for v in s: | O(N) | ||
| Copy | s.copy() | O(N) |
Sets have many more operations that are O(1) compared with lists and tuples. Not needing to keep values in a specific order (which lists/tuples require) allows for faster operations.
Frozen sets support all operations that do not mutate the data structure (and with the same complexity classes).
Dictionaries: dict and defaultdict
| Operation | Example | Complexity Class | Notes |
|---|---|---|---|
| Index | d[k] | O(1) | |
| Store | d[k] = v | O(1) | |
| Length | len(d) | O(1) | |
| Delete | del d[k] | O(1) | |
| get/setdefault | d.method | O(1) | |
| Pop | d.pop(k) | O(1) | |
| Pop item | d.popitem() | O(1) | |
| Clear | d.clear() | O(1) | similar to s = {} or = dict() |
| View | d.keys() | O(1) | same for d.values() |
| Construction | dict(…) | O(len(…)) | depends # (key,value) 2-tuples |
| Iteration | for k in d: | O(N) | all forms: keys, values, items |
So, most dict operations are O(1).
defaultdicts support all operations that dicts support, with the same complexity classes (because it inherits all the operations); this assumes that calling the constructor when a values isn’t found in the defaultdict is O(1) - which is true for int(), list(), set(), … (the things we commonly use)
Note that for i in range(...) is O(len(...)); so for i in range(1,10) is O(1).
If len(alist) is N, thenfor i in range(len(alist)):
is O(N) because it loops N times. Of course evenfor i in range (len(alist)//2):
is O(N) because it loops N/2 times, and dropping the constant 1/2 makes it O(N): the work doubles when the list length doubles.
Finally, when comparing two lists for equality, the complexity class above shows as O(N), but in reality we would need to multiply this complexity by O(==) where O(==) is the complexity class for checking whether two values in
the list are ==. If they are ints, O(==) would be O(1); if they are strings, O(==) in the worst case it would be O(len(string)). This issue applies any time an == check is done. We mostly will assume == checking on values in lists is O(1).
Composing Complexity Classes: Sequential and Nested Statements
In this section we will learn how to combine complexity class information about simple operations into complexity information about complex operations (composed from simple operations). The goal is to be able to analyze all the statements in a function/method to determine the complexity class of executing the function/method.
Law of Addition for big-O notation
O(f(n)) + O(g(n)) is O( f(n) + g(n) )
That is, we when adding complexity classes we bring the two complexity classes inside the O(…). Ultimately, O( f(n) + g(n) ) results in the bigger of the two complexity class (because we drop the lower added term). So,
O(N) + O(Log N) = O(N + Log N) = O(N)
because N is the faster growing function.
This rule helps us understand how to compute the complexity of doing some SEQUENCE of operations: executing a statement that is O(f(n)) followed by executing a statement that is O(g(n)). Executing both statements SEQUENTIALLY is O(f(n)) + O(g(n)) which is O( f(n) + g(n) ) by the rule above.
For example, if some function call f(…) is O(N) and another function call g(…) is O(N Log N), then doing the sequence
f(...) |
is O(N) + O(N Log N) = O(N + N Log N) = O(N Log N). Of course, executing the sequence (calling f twice)
f(...) |
is O(N) + O(N) which is O(N + N) which is O(2N) which is O(N).
Note that for an if statement like:
if test: assume complexity of test is O(T) |
The complexity class for the if is O(T) + max(O(B1),O(B2)). The test is always evaluated, and one of the blocks is always executed. In the worst case, the if will execute the block with the largest complexity. So, given
if test: complexity is O(N) |
The complexity class for the if is O(N) + max (O($N^2$),O(N))) = O(N) + O($N^2$) = O($N^2$). If the test had complexity class O($N^3$), then the complexity class for the if is O($N^3$) + max (O($N^2$),O(N))) = O($N^3$).
Law of Multiplication for big-O notation
O(f(n)) * O(g(n)) is O( f(n) * g(n) )
If we repeat an O(f(N)) process O(N) times, the resulting complexity is O(N) * O(f(N)) = O( Nf(N) ). An example of this is, if some function call f(…) is O($N^2$), then executing that call N times (in the following loop)for i in range(N):
f(...)
is O(N) * O($N^2$) = O($N*N^2$) = O($N^3$)
This rule helps us understand how to compute the complexity of doing some statement INSIDE A BLOCK controlled by a statement that is REPEATING it. We multiply the complexity class of the number of repetitions by the complexity class of the statement(s) being repeated.
Compound statements can be analyzed by composing the complexity classes of their constituent statements. For sequential statements the complexity classes are added; for statements repeated in a loop the complexity classes are multiplied.
An example
Let’s use the data and tools discussed above to analyze (determine their complexity classes) three different functions that each compute the same result:
Whether or not a list contains only unique values (no duplicates).
We will assume in all three examples that len(alist) is N.
Algorithm 1
A list is unique if each value in the list does not occur in any later indexes: alist[i+1:] is a list containing all values after the one at index i.
def is_unique1 (alist): |
The complexity class for executing the entire function is O(N) * O(N) + O(1) = O(N^2). So we know from the previous lecture that if we double the length of alist, this function takes 4 times as long to execute.
Note that in the worst case, we never return False and keep executing the loop, so this O(1) does not appear in the answer. Also, in the worst case the list slice is aliset[1:] which is O(N-1) = O(N).
Algorithm 2
A list is unique if when we sort its values, no ADJACENT values are equal. If there were duplicate values, sorting the list would put these duplicate values right next to each other (adjacent). Here we copy the list so as to not mutate (change the order of the parameter’s list) by sorting it: it turns out that copying the list does not increase the complexity class of the method.
def is_unique2 (alist): |
The complexity class for executing the entire function is given by the sum O(N) + O(N Log N) + O(N)*O(1) + O(1) = O(N + N Log N + O(N*1) + 1) = O(N + N Log N + N + 1) = O(N Log N + 2N + 1) = O(N Log N). So the complexity class for this algorithm/function is lower than the first algorithm, the is_unique1 function. For large N is_unique2 will eventually be faster.
Notice that the complexity class for sorting is dominant in this code: it does most of the work. If we double the length of alist, this function takes a bit more than twice the amount of time. In N Log N: N doubles and Log N gets a tiny bit bigger (i.e., Log 2N = 1 + Log N; e.g., Log 2000 = 1 + Log 1000 = 11, so compared to 1000 Log 1000, 2000 Log 2000 got 2.2 times bigger, or 10% bigger than just doubling).
Looked at another way if
$T(N) = c*(N Log N)$
then,
$T(2N) = c*(2N Log 2N)$ = $c*2N*(Log N + 1)$ = $c*2N Log N + c*2N$ = $2*T(N) + c*2N$
Or, computing the doubling signature
T(2N) c*2(N Log N) + c*2N 2 |
So, the ratio is 2 + a bit (and that bit gets smaller as N increases)
Algorithm 3
A list is unique if when we turn it into a set, its length is unchanged: if duplicate values were added to the set, its length would be smaller than the length of the list by exactly the number of duplicates in the list added to the set.
def is_unique3 (alist): |
The complexity class for executing the entire function is O(N) + O(1) = O(N + 1) = O(N). So the complexity class for this algortihm/function is lower than both the first and second algorithms/functions. If we double the length of alist, this function takes just twice the amount of time. We could write the body of this function more simply as:return len(set(alist)) == len(alist)
where evaluating set(alist) takes O(N) and then computing the two len’s and comparing them for equality are all O(1).
So the bottom line here is that there might be many algorithms/functions to solve some problem. If they are small, we can analyze them statically (looking at the code, not running it) to determine their complexity classes. For large problem sizes, the algorithm/function with the smallest complexity class will be best. For small problem sizes, complexity classes don’t determine which is best (we need to account for the constants and lower order terms when sizes are small), but we could run the functions (dynamic analysis, aka empirical analysis) to test which is fastest on small size.
Priority Queue
Using a Class (implementable 3 ways) Example:
We will now look at the solution of a few problems (combining operations on a priority queue: pq) and how the complexity class of the result is affected by three different classes/implementations of priority queues.
In a priority queue, we can add values and remove values to the data structure. A correctly working priority queue always removes the maximum value remaining in the priority queue. Think of a line/queue outside of a Hollywood nightclub, such that whenever space opens up inside, the most famous person in line gets to go in (the “highest priority” person), no matter how long less famous people have been standing in line (contrast this with first come/first serve, which is a regular -non priority- queue).
For the problems below, all we need to know is the complexity class of the “add” and “remove” operations.
| add | remove | |
|---|---|---|
| Implementation 1 | O(1) |
O(N) |
| Implementation 2 | O(N) |
O(1) |
| Implementation 3 | O(Log N) |
O(Log N) |
Implementation 1 adds the new value into the pq by appending the value at the rear of a list or the front of a linked list: both are O(1); it removes the highest priority value by scanning through the list or linked list to find the highest value, which is O(N), and then removing that value, also O(N) in the worst case (removing at the front of a list; at the rear of a linked list).
Implementation 2 adds the new value into the pq by scanning the list or linked list for the right spot to put it and putting it there, which is O(N). Lists store their highest priority at the rear (linked lists at the front); it removes the highest priority value from the rear for lists (or the front for linked lists), which is O(1).
Implementation 3, which is discussed in ICS-46, uses a binary heap tree (not a binary search tree) to implement both operations with “middle” complexity O(Log N): this complexity class greater than O(1) but less than O(N).
Problem 1
Suppose we wanted to use the priority queue to sort N values: we add N values in the pq and then remove all N values (first the highest, next the second highest, …). Here is the complexity of these combined operations for each implementation.
- Implementation 1:
$O(N)*O(1) + O(N)*O(N)$ = $O(N) + O(N^2)$ = $O(N^2)$ - Implementation 2:
$O(N)*O(N) + O(N)*O(1)$ = $O(N^2) + O(N)$ = $O(N^2)$ - Implementation 3:
$O(N)*O(Log N) + O(N)*O(Log N)$ = $O(N LogN) + O(N LogN)$ = $O(N LogN)$
Here, Implementation 3 has the lowest complexity class for the combined operations. Implementations 1 and 2 each do one operation quickly but the other slowly: both are done O(N) times. The slowest operation determines the complexity class, and both are equally slow. The complexity class O(Log N) is between O(1) and O(N); surprisingly, it is actually “closer” to O(1) than O(N), even though it does grow -because it grows so slowly; yes, O(1) doesn’t grow at all, but O(Log N) grows very slowly: the known Universe has about $ 10^{90} $ particles of matter, and $ Log_2(10^{90}) = Log_2 (10 ^ 3) ^ {30} \approx 30 * 10 = 300 $, which isn’t very big compared to $10^{90}$.
Problem 2
Suppose we wanted to use the priority queue to find the 10 biggest (of N) values: we would enqueue N values and then dequeue 10 values. Here is the complexity of these combined operations for each implementation..
- Implementation 1:
$O(N)*O(1) + O(10)*O(N)$ = $O(N) + O(N)$ = $O(N)$ - Implementation 2:
$O(N)*O(N) + O(10)*O(1)$ = $O(N^2) + O(1)$ = $O(N^2)$ - Implementation 3:
$O(N)*O(Log N) + O(10)*O(Log N)$ = $O(N LogN) + O(LogN)$ = $O(N LogN)$
Here, Implementation 1 has the lowest complexity for the combined operations. That makes sense, as the operation done O(N) times (add) is very simple (add to the end of a list/the front of a linked list is O(1)) and the operation done a constant number of times (10, independent of N) is the expensive operation (remove, which is O(N)). It even beats the complexity of Implementation 3. So, as N gets bigger, implementation 1 will eventually become faster than the other two for the “find the 10 biggest” task.
Kai’s comment:
For problem 2, the author came to a conclusion that, the brutal loop through the $N$ values for $K$ times, performs better than a heap based solution. It violates my intuition.
The questionable part is the cost of building a heap: $O(N LogN)$. The cost ofheapsortis the same, and by heapsorting an array, all the elements are sorted. Then why should we perform an operation, that is close to heapsort, to find top $K$ elements?
I will discuss this in another blog Solve Biggest K Problem By Heap, In Right Way
So, the bottom line here is that sometimes there is NOT a “best all the time” implementation for a data structure. We need to know what problem we are solving (the complexity classes of all the operations in various implementations and the number of times we must do these operations) to choose the most efficient implementation for solving the problem.

